Daftar Isi:
- Klik di sini 👉Arus Listrik
- Klik di sini 👉Hukum Ohm dan Hambatan Listrik
- Klik di sini 👉Rangkaian Listrik Arus Searah (DC)
- Klik di sini 👉Energi dan Daya Listrik
- Klik di sini 👉Alat Ukur Listrik
- Klik di sini 👉Pemanfaatan Energi Listrik dalam Kehidupan Sehari-...
- Klik di sini 👉Menghitung Biaya Sewa Energi Listrik
Gambar 8.8 memperlihatkan skema sebuah lampu, sakelar, dan baterai yang satu sama lain terhubung oleh kabel/kawat. Ketika sakelar masih terbuka, Gambar 8.8(a), arus listrik belum mengalir sehingga lampu belum menyala (padam). Sebaliknya, ketika sakelar disambungkan, Gambar 8.8(b), arus mengalir dari kutub positif baterai ke kutub negatif baterai melalui kabel dan lampu sehingga lampu menyala. Gambar 8.8(a) disebut rangkaian listrik terbuka, sedangkan Gambar 8.8(b) disebut rangkaian listrik tertutup. Rangkaian seperti ini secara umum disebut rangkaian listrik arus searah. Rangkaian listrik arus searah yang terdiri dari sebuah baterai dan sebuah beban (misalnya hambatan dan lampu) disebut rangkaian listrik sederhana.
1. GGL, Hambatan Dalam, dan Tegangan Jepit Baterai
Baterai merupakan sumber energi arus searah. Energi listrik yang dihasilkan baterai berasal dari energi kimia. Selain baterai, sumber energi listrik lainnya adalah generator. Secara umum, alat yang dapat mengubah suatu bentuk energi lain menjadi energi listrik disebut sumber gaya gerak listrik (GGL). GGL adalah beda potensial antarterminal sumber tegangan (bateai atau generator), ketika tidak ada arus yang mengalir pada rangkaian luar. Simbol GGL adalah E.
Anda mungkin pernah mengalami bahwa ketika arus ditarik dari baterai, tegangan pada terminal baterai turun di bawah GGLnya. Sebagai contoh, ketika Anda menstarter mesin mobil, dengan lampu depan masih menyala, lampu menjadi redup sesaat. Ini terjadi karena starter menarik arus besar sehingga tegangan baterai menjadi turun. Penurunan tegangan ini terjadi karena reaksi kimia dalam baterai tidak cukup menyuplai muatan untuk mempertahankan GGLnya menjadi penuh. Jadi, baterai sendiri memiliki hambatan dalam r. Dalam rangkaian listrik, baterai disimbolkan seperti pada Gambar 8.9. Tegangan antara titik a dan b disebut tegangan terminal Vab. Ketika baterai tidak mengeluarkan arus, Vab = E. Akan tetapi, ketika baterai menge- luarkan arus, tegangan terminal baterai turun sebesar Ir. Jadi, Vab = E – Ir. Tegangan terminal baterai ketika baterai mengeluarkan arus disebut dengan tegangan jepit.
2. Hukum-Hukum Kirchhoff dan Penerapannya
a. Hukum Arus Kirchhoff
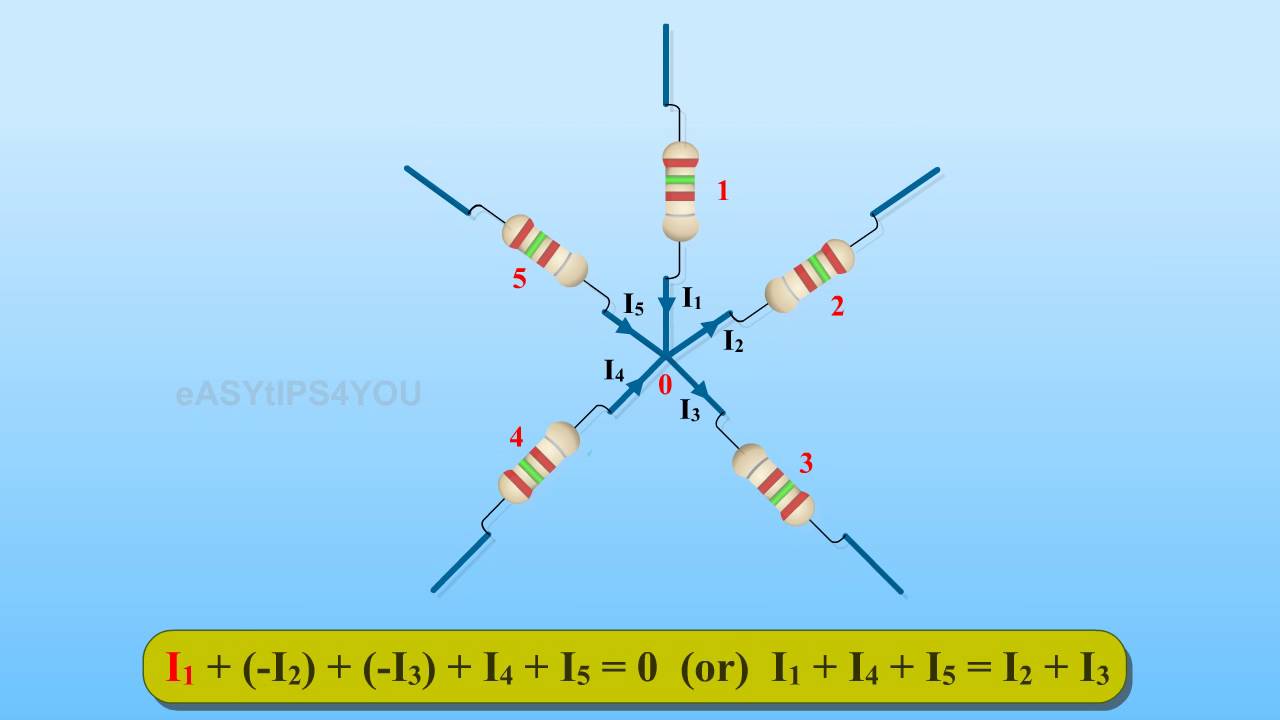
Hukum Arus Kirchhoff membicarakan arus listrik pada titik percabangan kawat. Tinjau sebuah titik percabangan kawat, sebut titik A, seperti yang diperlihatkan pada Gambar 8.10.
Arus I1 dan I2 menuju (masuk ke) titik A, sedangkan I3 dan I4 menjauhi (keluar dari) titik A. Jika aliran arus dianalogikan sebagai aliran air dalam pipa, Anda tentu akan yakin bahwa jumlah aliran air sebelum melewati titik A akan sama dengan jumlah air sesudah melewati titik A. Demikian pula dengan arus listrik, jumlah arus listrik yang menuju (masuk ke) titik percabangan (titik A) sama dengan jumlah arus yang menjauhi (keluar dari) titik percabangan tersebut. Dengan demikian, pada Gambar 8.10, secara matematis diperoleh
yang berarti bahwa jumlah arus listrik pada suatu titik percabangan sama dengan nol. Persamaan (8–10) disebut Hukum Pertama Kirchhoff atau Hukum Arus Kirchhoff. Perlu diingat bahwa ketika Anda menggunakan Persamaan (8–10), arus yang masuk ke titik percabangan diberi tanda positif, sedangkan arus yang keluar dari titik percabangan diberi tanda negatif.
b. Hukum Tegangan Kirchhoff
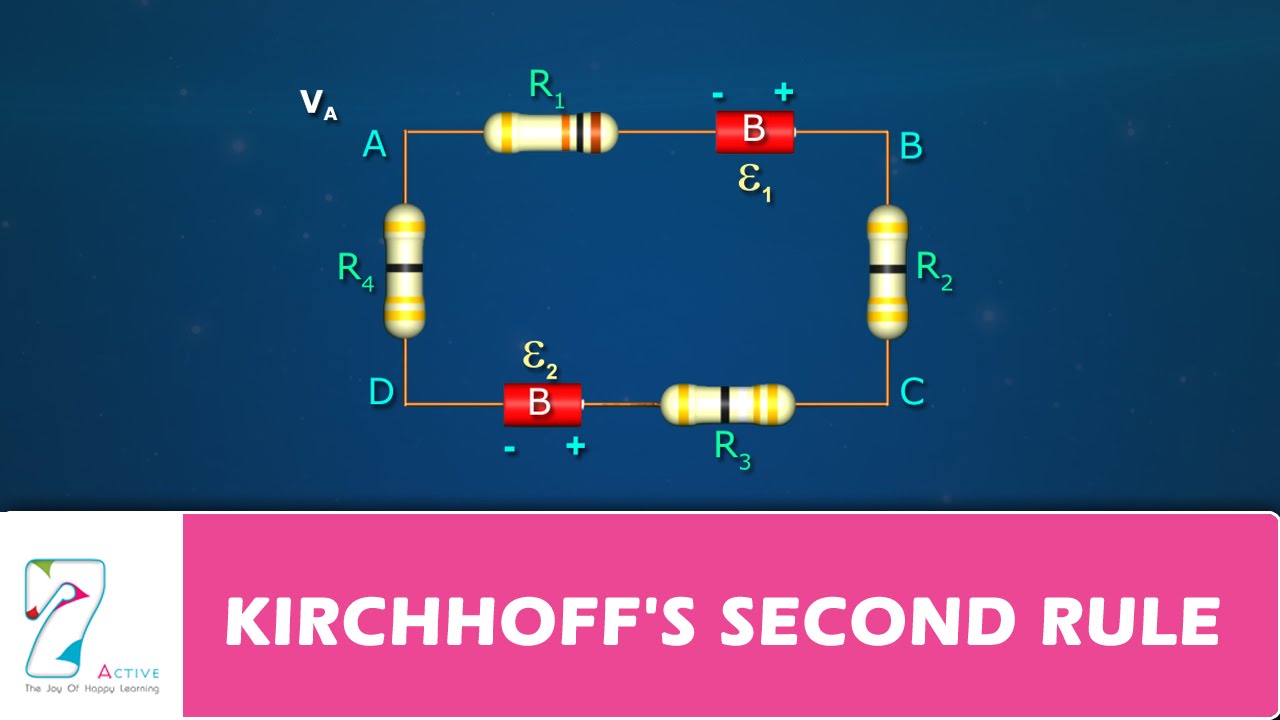
Hukum Tegangan Kirchhoff didasarkan pada Hukum Kekekalan Energi. Ketika muatan listrik q berpindah dari potensial tinggi ke potensial rendah dengan beda potensial V, energi muatan itu akan turun sebesar qV. Sekarang tinjau rangkaian listrik, seperti diperlihatkan pada Gambar 8.11.
Baterai dengan tegangan terminal V akan melepas muatan q dengan energi qV sedemikian sehingga mampu bergerak pada lintasan tertutup (loop) abcda. Ketika muatan q melintasi resistansi R1, energi muatan ini akan turun sebesar qV1. Demikian pula ketika melintasi R2 dan R3, masing-masing energinya turun sebesar qV2 dan qV3. Total penurunan energi muatan adalah qV1 + qV2 + qV3.
Sesuai dengan Hukum Kekekalan Energi, penurunan ini harus sama dengan energi yang dilepaskan oleh baterai, qV. Dengan demikian berlaku
c. Penerapan Hukum Kirchhoff pada Rangkaian Sederhana
Rangkaian sederhana adalah rangkaian yang terdiri dari satu loop. Sebagai contoh, tinjau rangkaian pada Gambar 8.12.
Tidak ada titik percabangan di sini sehingga arus pada setiap hambatan sama, yakni I dengan arah seperti pada gambar. Pilih loop a-b-c-d-a. Ketika Anda bergerak dari a ke b, Anda menemui kutub negatif baterai terlebih dahulu sehingga GGLnya ditulis Vab = E1. Ketika Anda melanjutkan gerakan dari b ke c, Anda mendapati arah arus sama dengan arah gerakan Anda sehingga tegangan pada R1 diberi tanda positif, yakni Vbc = +IR1. Dari c ke d kembali Anda menemui GGL dan kali ini kutub positifnya terlebih dahulu sehingga diperoleh Vcd = +E2. Selanjutnya, tegangan antara d dan a diperoleh Vda = +IR2. Hasil tersebut kemudian dimasukkan ke dalam Persamaan (8–11).
Dengan demikian, untuk rangkaian listrik sederhana, besarnya arus listrik yang mengalir pada rangkaian dapat dicari menggunakan Persamaan (8–12). Akan tetapi, jangan lupa ketika memasukkan nilai GGLnya, Anda harus tetap memerhatikan tanda GGL tersebut.
d. Penerapan Hukum-hukum Kirchhoff pada Rangkaian Majemuk
Rangkaian majemuk adalah rangkaian arus searah yang lebih dari satu loop. Salah satu cara untuk menganalisis rangkaian majemuk adalah analisis loop. Analisis ini pada dasarnya menerapkan Hukum-hukum Kirchhoff, baik tentang arus maupun tegangan. Berikut adalah langkah- langkah untuk menganalisis rangkaian majemuk pada Gambar 8.13 menggunakan analisis loop.
- Tandai titik-titik sudut atau titik cabang rangkaian, misalnya titik a, b, c, d, e, dan f.
- Tentukan arah arus pada tiap cabang, sebarang saja, sesuai keinginan Anda. Lalu, gunakan Persamaan (8–10) untuk mendapatkan persamaan arusnya.
- Tentukan titik tempat Anda mulai bergerak dan lintasan yang akan Anda lalui. Misalnya, Anda ingin memulai dari titik a menuju titik b, c, dan d lalu ke a lagi maka yang dimaksud satu loop adalah lintasan a-b-c-d-a. Lakukan hal yang serupa untuk loop c-d-e-f-c.
- Jika Anda melewati sebuah baterai dengan kutub positif terlebih dahulu, GGL E diberi tanda positif (+E). Sebaliknya, jika kutub negatif lebih dulu, GGL E diberi tanda negatif ( E).
- Jika Anda melewati sebuah hambatan R dengan arus I searah loop Anda, tegangannya diberi tanda positif (+IR). Sebaliknya, jika arah arus I berlawanan dengan arah loop Anda, tegangannya diberi tanda negatif (IR).
- Masukkan hasil pada langkah 3 ke Persamaan (8–11).
- Dari beberapa persamaan yang Anda dapatkan, Anda dapat melakukan eliminasi untuk memperoleh nilai arus pada tiap cabang.
e. Penerapan Hukum Arus Kirchhoff dan Hukum Ohm pada Rangkaian Majemuk
Selain analisis loop, analisis simpul juga dapat digunakan untuk menganalisis rangkaian majemuk. Analisis ini menerapkan Hukum Arus Kirchhoff dan Hukum Ohm. Berikut adalah langkah-langkah untuk menerapkan analisis simpul pada rangkaian majemuk yang diperlihatkan pada Gambar 8.14.
1)Pilih salah satu titik (simpul), misal A, sebagai acuan dengan tegangan nol (ground) dan titik (simpul) lainnya, misal B, anggap memiliki tegangan V terhadap ground, yakni VBA = V.
2) Pilih semua arus pada tiap cabang, yakni I1, I2, dan I3, berarah dari B ke A. 3) Jika pada cabang arus terdapat baterai (GGL), perhatikan kutub baterai yang ditemui arah arus. Jika arus yang Anda misalkan masuk ke kutub positif baterai, arus pada cabang tersebut memenuhi persamaan
6) Untuk mendapatkan arus pada tiap cabang, Anda tinggal memasukkan nilai V hasil langkah 5 ke persamaan I pada langkah 3.